Buenas tardes, escribo por aquí por la duda del siguiente ejercicio, en cuanto al proceso de razonamiento:
Práctico 3 - Inducción Completa. Ejercicio 7: Demuestre que en la lista de inscriptos al curso de Matemática Discreta I hay una
cantidad par de estudiantes que tienen una cantidad impar de amigos inscriptos en el mismo curso.
Bien, hay distintas estrategias de resolución:
1) Modelar el problema como un grafo (los estudiantes son vértices, las amistades son artistas) y luego aplicando un resultado fundamental de teoría de grafos, que veremos más adelante en este mismo curso que habla de la relación entre el grado de los vértices y la cantidad de aristas.
2) Utilizando funciones y aritmética modular (paridad).
3) Utilizando inducción completa.
Aquí voy a presentar el método 2), y los invito a que piensen el 3). El método 1) lo veremos más adelante en el curso.
-----
Demostración usando funciones y paridad.
Sea S el conjunto de estudiantes inscritos en el curso. Para cada par de estudiantes i, j ∈ S, definimos una función f tal que:
f(i, j) = 1 si i y j son amigos
f(i, j) = 0 en caso contrario
Notemos que f(i, j) = f(j, i) para todo i, j ∈ S porque la amistad es simétrica.
Para cada estudiante i ∈ S, el número de amigos que tiene es:
A(i) = ∑(j ∈ S) f(i, j)
Queremos demostrar que hay una cantidad par de estudiantes con A(i) impar.
Consideremos la suma doble:
∑(i ∈ S) ∑(j ∈ S) f(i, j)
Esta suma cuenta cada amistad exactamente dos veces (una vez desde i hacia j y otra desde j hacia i).
Por lo tanto:
∑(i ∈ S) ∑(j ∈ S) f(i, j) = ∑(i ∈ S) A(i) = 2 · (número total de amistades)
El número total de amistades es un entero, así que ∑(i ∈ S) A(i) es un número par.
Ahora, dividamos los estudiantes en dos grupos:
- S_impar: estudiantes con un número impar de amigos
- S_par: estudiantes con un número par de amigos
Entonces:
∑(i ∈ S) A(i) = ∑(i ∈ S_impar) A(i) + ∑(i ∈ S_par) A(i)
Como ∑(i ∈ S_par) A(i) es una suma de números pares, esta suma es par.
Y dado que ∑(i ∈ S) A(i) es par, necesariamente ∑(i ∈ S_impar) A(i) también debe ser par.
Pero ∑(i ∈ S_impar) A(i) es una suma de números impares. La única forma en que una suma de números impares puede ser par es si hay una cantidad par de sumandos.
Por lo tanto, |S_impar| (el número de estudiantes con una cantidad impar de amigos) debe ser par.
1) Modelar el problema como un grafo (los estudiantes son vértices, las amistades son artistas) y luego aplicando un resultado fundamental de teoría de grafos, que veremos más adelante en este mismo curso que habla de la relación entre el grado de los vértices y la cantidad de aristas.
2) Utilizando funciones y aritmética modular (paridad).
3) Utilizando inducción completa.
Aquí voy a presentar el método 2), y los invito a que piensen el 3). El método 1) lo veremos más adelante en el curso.
-----
Demostración usando funciones y paridad.
Sea S el conjunto de estudiantes inscritos en el curso. Para cada par de estudiantes i, j ∈ S, definimos una función f tal que:
f(i, j) = 1 si i y j son amigos
f(i, j) = 0 en caso contrario
Notemos que f(i, j) = f(j, i) para todo i, j ∈ S porque la amistad es simétrica.
Para cada estudiante i ∈ S, el número de amigos que tiene es:
A(i) = ∑(j ∈ S) f(i, j)
Queremos demostrar que hay una cantidad par de estudiantes con A(i) impar.
Consideremos la suma doble:
∑(i ∈ S) ∑(j ∈ S) f(i, j)
Esta suma cuenta cada amistad exactamente dos veces (una vez desde i hacia j y otra desde j hacia i).
Por lo tanto:
∑(i ∈ S) ∑(j ∈ S) f(i, j) = ∑(i ∈ S) A(i) = 2 · (número total de amistades)
El número total de amistades es un entero, así que ∑(i ∈ S) A(i) es un número par.
Ahora, dividamos los estudiantes en dos grupos:
- S_impar: estudiantes con un número impar de amigos
- S_par: estudiantes con un número par de amigos
Entonces:
∑(i ∈ S) A(i) = ∑(i ∈ S_impar) A(i) + ∑(i ∈ S_par) A(i)
Como ∑(i ∈ S_par) A(i) es una suma de números pares, esta suma es par.
Y dado que ∑(i ∈ S) A(i) es par, necesariamente ∑(i ∈ S_impar) A(i) también debe ser par.
Pero ∑(i ∈ S_impar) A(i) es una suma de números impares. La única forma en que una suma de números impares puede ser par es si hay una cantidad par de sumandos.
Por lo tanto, |S_impar| (el número de estudiantes con una cantidad impar de amigos) debe ser par.
Para ayudar a entender la resolución, comparto tres ejemplos numéricos concretos. Cada ejemplo está acompañado de un diagrama para visualizar las amistades.
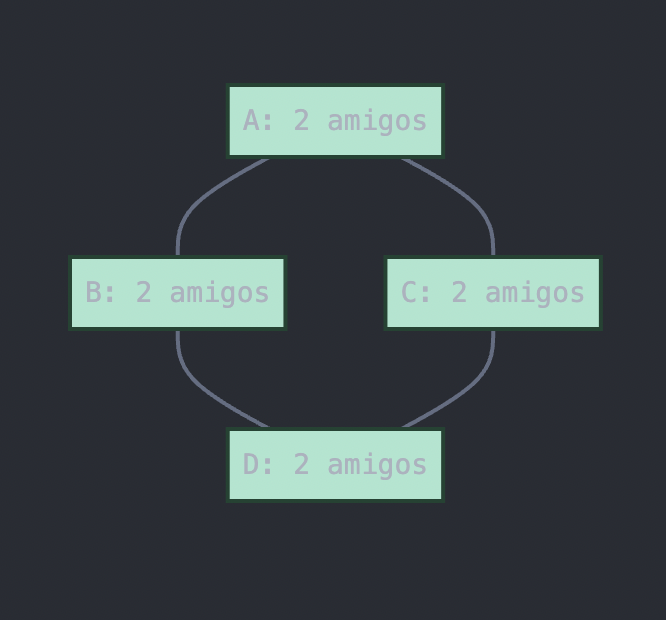
### Ejemplo 1: Clase con 4 estudiantes
Consideremos una clase con 4 estudiantes: A, B, C y D.
Definimos estas relaciones de amistad:
- A es amigo de B y C
- B es amigo de A y D
- C es amigo de A y D
- D es amigo de B y C
Contando el número de amigos:
- Estudiante A tiene 2 amigos (B y C) → número par de amigos
- Estudiante B tiene 2 amigos (A y D) → número par de amigos
- Estudiante C tiene 2 amigos (A y D) → número par de amigos
- Estudiante D tiene 2 amigos (B y C) → número par de amigos
En este ejemplo, 0 estudiantes tienen un número impar de amigos, lo cual es un número par (0 es par).
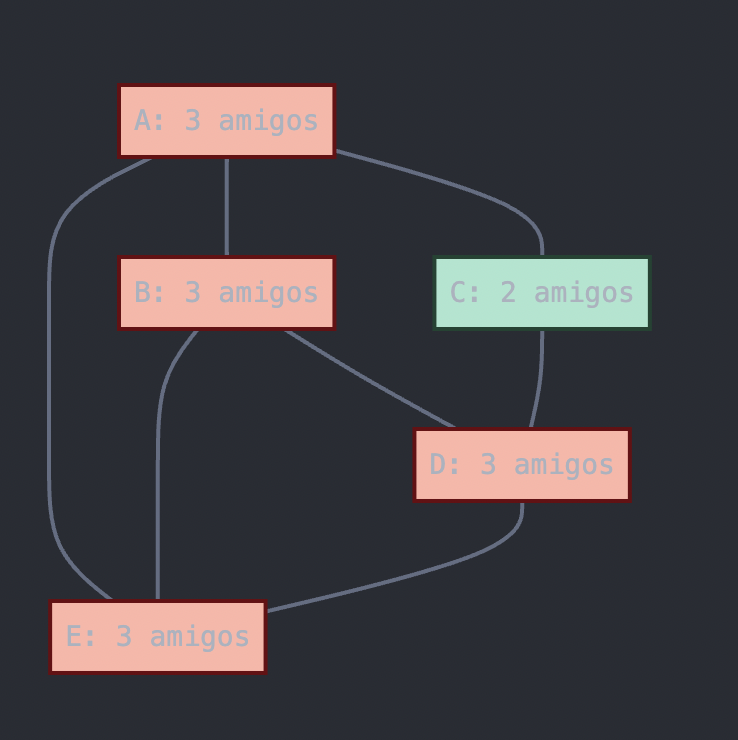
### Ejemplo 2: Clase con 5 estudiantes
Añadamos un estudiante E al ejemplo anterior:
- A es amigo de B, C y E
- B es amigo de A, D y E
- C es amigo de A y D
- D es amigo de B, C y E
- E es amigo de A, B y D
Contando amigos:
- Estudiante A tiene 3 amigos → número impar de amigos
- Estudiante B tiene 3 amigos → número impar de amigos
- Estudiante C tiene 2 amigos → número par de amigos
- Estudiante D tiene 3 amigos → número impar de amigos
- Estudiante E tiene 3 amigos → número impar de amigos
En este caso, 4 estudiantes (A, B, D, E) tienen un número impar de amigos, lo cual es un número par (4 es par).
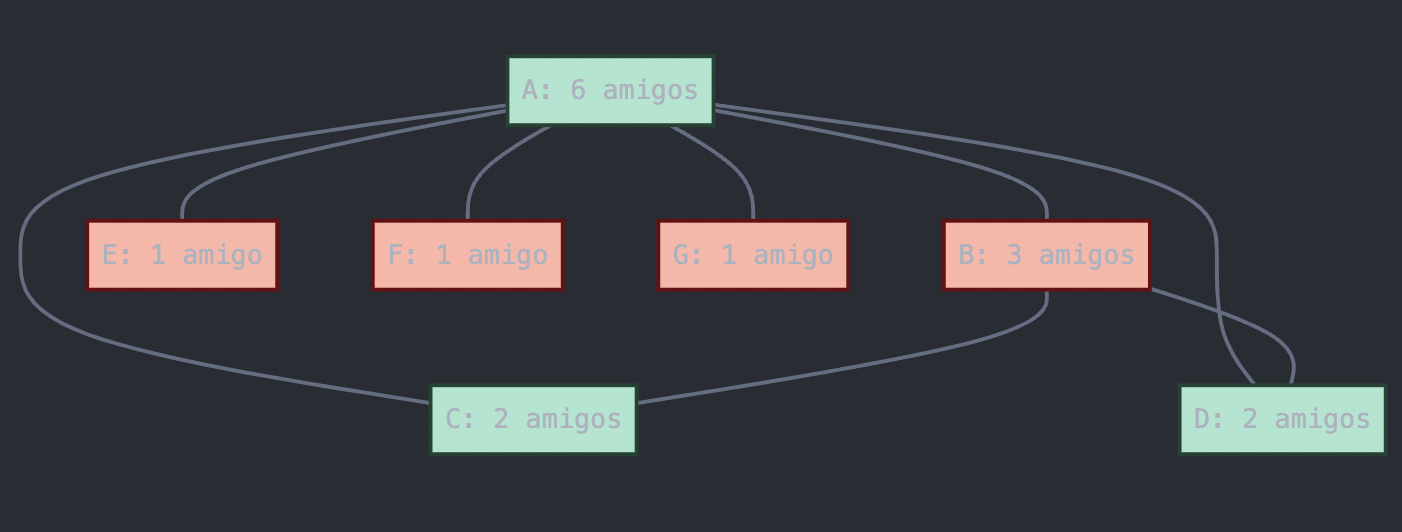
### Ejemplo 3: Red de amistad "desequilibrada" con 7 estudiantes
Consideremos un patrón de amistad diferente:
- A es amigo de todos los demás (B, C, D, E, F, G)
- B es amigo de A, C y D
- C es amigo de A y B
- D es amigo de A y B
- E es amigo solo de A
- F es amigo solo de A
- G es amigo solo de A
Contando amigos:
- Estudiante A tiene 6 amigos → número par de amigos
- Estudiante B tiene 3 amigos → número impar de amigos
- Estudiante C tiene 2 amigos → número par de amigos
- Estudiante D tiene 2 amigos → número par de amigos
- Estudiante E tiene 1 amigo → número impar de amigos
- Estudiante F tiene 1 amigo → número impar de amigos
- Estudiante G tiene 1 amigo → número impar de amigos
En este caso, 4 estudiantes (B, E, F, G) tienen un número impar de amigos, lo cual es nuevamente un número par.
### Ejemplo 1: Clase con 4 estudiantes
Consideremos una clase con 4 estudiantes: A, B, C y D.
Definimos estas relaciones de amistad:
- A es amigo de B y C
- B es amigo de A y D
- C es amigo de A y D
- D es amigo de B y C
Contando el número de amigos:
- Estudiante A tiene 2 amigos (B y C) → número par de amigos
- Estudiante B tiene 2 amigos (A y D) → número par de amigos
- Estudiante C tiene 2 amigos (A y D) → número par de amigos
- Estudiante D tiene 2 amigos (B y C) → número par de amigos
En este ejemplo, 0 estudiantes tienen un número impar de amigos, lo cual es un número par (0 es par).
### Ejemplo 2: Clase con 5 estudiantes
Añadamos un estudiante E al ejemplo anterior:
- A es amigo de B, C y E
- B es amigo de A, D y E
- C es amigo de A y D
- D es amigo de B, C y E
- E es amigo de A, B y D
Contando amigos:
- Estudiante A tiene 3 amigos → número impar de amigos
- Estudiante B tiene 3 amigos → número impar de amigos
- Estudiante C tiene 2 amigos → número par de amigos
- Estudiante D tiene 3 amigos → número impar de amigos
- Estudiante E tiene 3 amigos → número impar de amigos
En este caso, 4 estudiantes (A, B, D, E) tienen un número impar de amigos, lo cual es un número par (4 es par).
### Ejemplo 3: Red de amistad "desequilibrada" con 7 estudiantes
Consideremos un patrón de amistad diferente:
- A es amigo de todos los demás (B, C, D, E, F, G)
- B es amigo de A, C y D
- C es amigo de A y B
- D es amigo de A y B
- E es amigo solo de A
- F es amigo solo de A
- G es amigo solo de A
Contando amigos:
- Estudiante A tiene 6 amigos → número par de amigos
- Estudiante B tiene 3 amigos → número impar de amigos
- Estudiante C tiene 2 amigos → número par de amigos
- Estudiante D tiene 2 amigos → número par de amigos
- Estudiante E tiene 1 amigo → número impar de amigos
- Estudiante F tiene 1 amigo → número impar de amigos
- Estudiante G tiene 1 amigo → número impar de amigos
En este caso, 4 estudiantes (B, E, F, G) tienen un número impar de amigos, lo cual es nuevamente un número par.
Muchas gracias profesor.