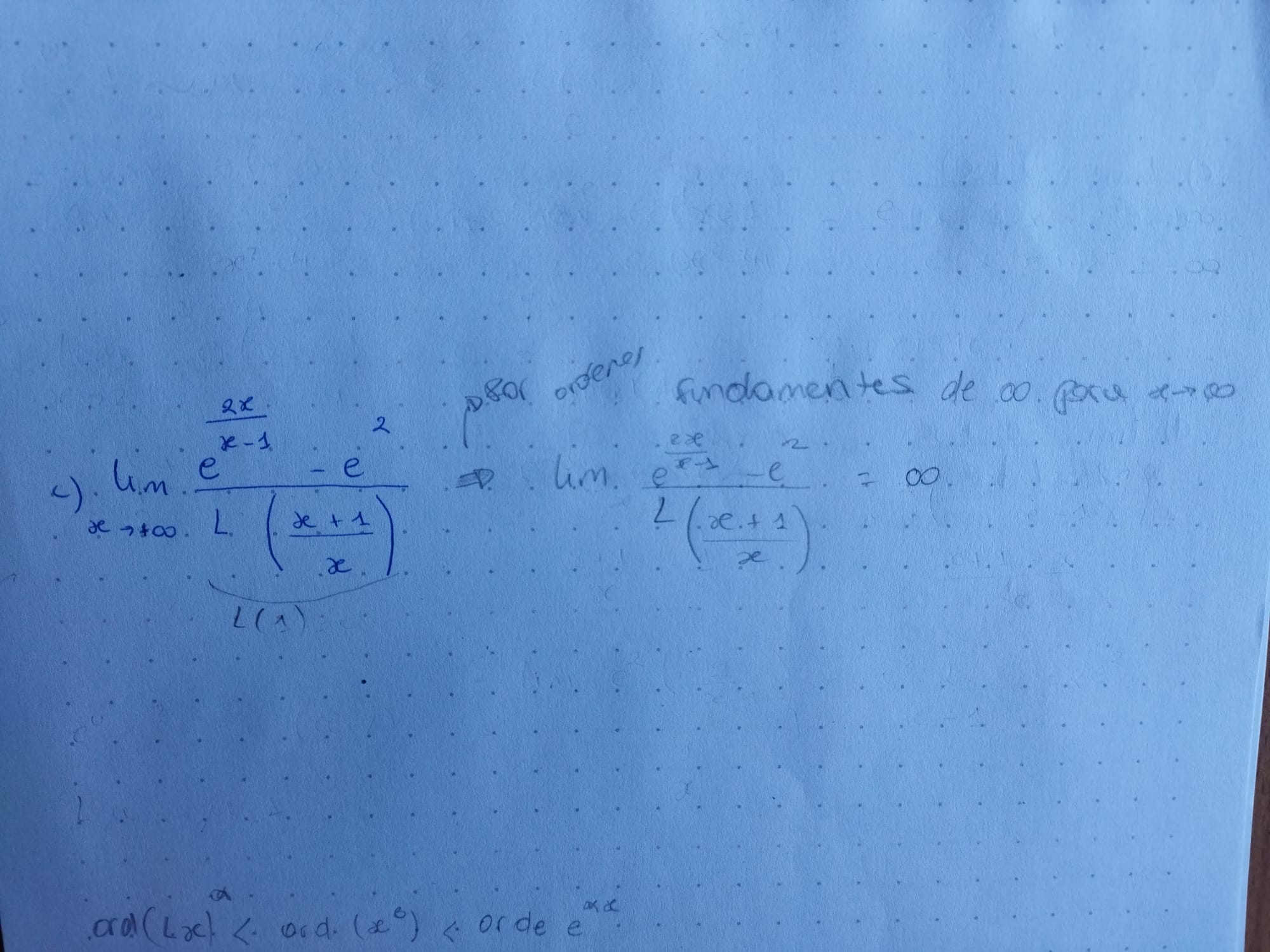m1: Practico 1. ej 11b y c

Hola, tengo una duda sobre como resolver los límites.

En el 11b) se puede aplicar infinitesimos equivalente en el numerador? ( Cómo se muestra en la imagen adjuntada ).

De ser así , se pueden aplicar siempre que tienda a cero ? Y sin importar si es una indeterminación? O cómo es ?

En el 11c) yo utilice órdenes fundamentales de infinitos para x tendiendo a infinito. Siguiendo con lo que aparece en la tabla de límites, como el de abajo tiene mayor orden que el de arriba tendería a infinito. Tengo la misma duda que en el de arriba, no sé si la aplicación es correcta y cuáles son los casos en los que se puede aplicar.

Re: Practico 1. ej 11b y c

por Faget Ignacio - terça-feira, 18 abr. 2023, 12:13

Buenas,

respondo la 11b)

Lo primero que hay que ver es cual es la definición de un infinitésimo.

Infinitesimo: Dada un función f(x) es un infinitésimo para $x \rightarrow a$ donde a puede ser finito o infinito, si $lim_{x\rightarrow a } f(x) = 0$ .

Ejemplo:

Sea

$f(x) = e^{x}$ , es un infinitésimo para

$x \rightarrow -\infty$ ya que $lim_{x\rightarrow -\infty } e^{x} = 0$ .

Luego hay que ver cual es la definición de infinitésimos equivalentes.

Infinitésimos equivalente: Dada 2 infinitesimos f y g (f y g estan bajo la condición de la definición anterior) se dicen equivalentes para $x \rightarrow a$ , si

$lim_{x\rightarrow a } \frac{f(x)}{g(x)} = 1$ ,por lo tanto se dice que $f \sim g$ para $x \rightarrow a$

Observación: A partir de la definición anterior sale la proposición de que

$lim_{x \rightarrow 0 } \frac{e^x -1}{x}$ entonces

$e^{x-1} \sim x$

No necesariamente puedes usar infinitésimos equivalentes cuando la indeterminación es 0/0, va un ejemplo que ilustra esto. \\

Ejemplo:

$lim_{x \rightarrow +\infty } { (4x^{2} -1) ( L(\frac{x+2}{x}) ) }$ =

$\infty .0$ (indet)

Podemos decir que

$L(\frac{x+2}{x})$ es un infinitésimo para

$x \rightarrow +\infty$ , ya que el límite da 0, y además

$L(\frac{x+2}{x}) \sim \frac{x+2}{x} -1$ son infinitésimos equivalentes para

$x \rightarrow +\infty$ ya que el límite del cociente entre ellos da 1 con

$x \rightarrow +\infty$ .

Entonces,

$lim_{x \rightarrow +\infty } {(4x^{2} -1)( L(\frac{x+2}{x}) )} = lim_{x \rightarrow +\infty } {(4x^{2} -1)(\frac{2}{x}) } = +\infty$

Con respecto a lo que hiciste en el ejercicio, el resultado es correcto. En la primer parte te das cuenta que el numerador es un infinitésimo para

$x\rightarrow 2$ , la idea ahí es sacar factor común e, para que te quede una expresión que también es un infinitésimo y al que es conocido el infinitesmo equivalente. Luego todo el procedimiento esta bien.

En otro mensaje abajo respondo el 11c)

Atte. Ignacio

Re: Practico 1. ej 11b y c

por Faget Ignacio - terça-feira, 18 abr. 2023, 12:59

Sigo con el 11c)

$lim_{x \rightarrow +\infty} \frac{ e^{\frac{2x}{x-1}} -e^2 }{ L(\frac{x+1}{x}) }$ es un indet 0/0 .

Como es una indeterminación 0/0 deducimos que tanto el numerador como el denominador es un infinitésimo para

${x \rightarrow +\infty}$ , ya que sus líimites dan 0.

Primero con el numerador, la idea es buscar un infinitésimo equivalente para esta expresión

$e^{\frac{2x}{x-1}} -e^2 = e^{2}( e^{\frac{2x}{x-1} -2} - 1) = e^{2}( e^{\frac{2}{x-1}} - 1)$ , por

lo tanto el infinitésimo equivalente de

$e^{\frac{2}{x-1}} - 1 \sim \frac{2}{x-1}$ , entonces del numerador se obtiene la expresión

$e^{2}(\frac{2}{x-1})$ .

Luego trabajamos con el denominador, de igual manera que lo hacemos con el numerador, como la indeterminación es 0/0,

$L(\frac{x+1}{x})$ es un infinitésimo para {x \rightarrow +\infty}, ya que su límite da 0.

Usando

$L(\frac{x+1}{x}) \sim \frac{x+1}{x} -1 = \frac{1}{x}$ .

En conclusión el límite a calcular ahora es:

$lim_{x \rightarrow +\infty} \frac{e^{2}(\frac{2}{x-1})}{\frac{1}{x}} = 2e^{2}$

Con respecto a lo de los ordenes de infinito, eso se usa cuando el límite de las funciones tendiendo a infinito da infinito, y lo que se hace es compara los ordenes a los efectos de ver cual predomina. En este caso las funciones se van a 0 cuando

$x \rightarrow +\infty$ por lo que nos esta diciendo que ambas funciones son infinitésimos para

$x \rightarrow +\infty$ .

Atte. Ignacio