
Recordemos la noción de error cuadrático medio (mean squared error, MSE).
Def (MSE). El error cuadrático medio (MSE) de un estimador \(W\) de un parámetro \(\theta\) es la función de \(\theta\) definida como \(E_\theta(W - \theta)^2\).
El MSE nos da una idea de la calidad de un estimador. Es decir, el MSE mide el promedio de la diferencia al cuadrado entre el estimador \(W\) y el parámetro \(\theta\).
Conviene introducir el bias de un estimador puntual para darle una interpetación al MSE.
Def. (bias). El bias de un estimador puntual \(W\) de un parámetro \(\theta\) es la diferencia entre el valor esperado de \(W\) y de \(\theta\). Es decir, \[ Bias_\theta W := E_\theta W - \theta. \]
Nótese que podemos realizar la manipulación siguiente:
\[ E_\theta(W - \theta)^2 = E_\theta(W^2) + \theta^2 - 2\theta E_\theta(W) \\ = (E_\theta(W^2)-(E_\theta(W))^2) + (\theta^2 - 2\theta E_\theta(W) + (E_\theta(W))^2 \\ = Var_\theta(W) + (Bias_\theta W)^2. \] En consecuencia, el MSE se puede interpretar como la suma de dos términos, el término \(Var_\theta(W)\) que mide la precisión (variabilidad del estimador), y el término \(Bias_\theta W\) que mide la exactitud (bias).
Recordemos la notación utilizada en estimación Bayesiana. Sea \(\pi(\theta)\) la distribución a priori del parámetro \(\theta\). Sea \(f(x\vert \theta)\) la distribución de la muestra. Notamos con \(\pi(\theta \vert x)\) a la distribución a posteriori, es decir, la distribución condicional de \(\theta\) dado el valor muestral \(x\). Notamos con \(m(x)\) a la distribución marginal de \(X\), es decir,
\[ m(x) = \int f(x\vert \theta) \pi(\theta)d\theta. \]
Nótese que la distribución a posteriori es
\[ \pi(\theta \vert x) = f(x \vert \theta) \pi(\theta) / m(x). \]
La distribución a posteriori, \(\pi(\theta \vert x)\), se puede utilizar para estudiar el parámetro \(\theta\), por ejemplo como estimdor puntual de \(\theta\) puedo tomar la media de la distribución a posteriori.
A continuación hacemos una recapitulacion de la distribución beta. \(Beta(\alpha, \beta)\) es una familia de distribuciónes continuas en el intervalo \((0, 1)\), indexada por dos parámetros \(\alpha\) y \(\beta\) con pdf \[ f(x \vert \alpha, \beta) = \dfrac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1},\quad 0<x<1,\quad \alpha, \beta > 0. \]
Aqui \(B(\alpha, \beta)\) denota la función beta, que se define en forma integral como
\[ B(\alpha, \beta) = \int_0^1 x^{\alpha - 1} (1-x)^{\beta - 1} dx. \]
Prop. (Relación entre la función beta y la función gamma). Recuerde que la función Gamma (forma integral de Euler) es \[ \Gamma(z) = \int_0^\infty e^{-t} t^{z-1} dt,\qquad ℜ(z) > 0. \] Se verifica que: \[ B(\alpha, \beta) = \dfrac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}. \]
Prueba. Escribimos el producto de dos funciones gamma:
\[ \Gamma(x)\Gamma(y) = \int_{u=0}^\infty e^{-u}u^{x-1}du \cdot \int_{v=0}^\infty e^{-v}v^{x-1}dv \\ = \int_{v=0}^\infty \int_{u=0}^\infty e^{-v-u}u^{x-1} v^{x-1} du dv. \]
Consideremos el cambio de variables \(u = f(z, t) = zt\) y \(v = g(z, t) = z(1-t)\). Entonces \(u = zt = v t / (1-t)\). El determinante de la matriz Jacobiana del cambio de variable es: \[ \vert J(v, z) \vert = -z. \]
El producto \(\Gamma(x)\Gamma(y)\) es
\[ \Gamma(x)\Gamma(y) = \int_{z=0}^\infty \int_{t=0}^1 e^{-z} (zt)^{x-1}(z(1-t))^{y-1} z dt dz \\ = \int_{z=0}^\infty e^{-z} z^{x+y-1} dz \int_{t=0}^1 t^{x-1} (1-t)^{y-1}dt. \\ = \Gamma(x+y) B(x, y). \] \(\square\)
A continuación calculamos los momentos de la distribución beta.
Prop. (Momentos de la distribución beta). Sea \(n\) un entero tal que \(n > -\alpha\). Entonces: \[ E(X^n) = \dfrac{\Gamma(\alpha + n)\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + n)\Gamma(\alpha)} \] En particular, para \(n=1\) y \(n=2\) tenemos que \[ E(X) = \dfrac{\Gamma(\alpha + 1)\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + 1)\Gamma(\alpha)} = \dfrac{\alpha}{\alpha + \beta}, \] \[ E(X^2) = \dfrac{\Gamma(\alpha + 2)\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + 2)\Gamma(\alpha)} = \dfrac{\alpha(\alpha+1)}{(\alpha + \beta + 1)(\alpha + \beta)}. \] y \[ Var(X) = \dfrac{\alpha \beta}{(\alpha + \beta + 1)(\alpha + \beta)^2}. \]
Prueba. Por definición, \[ E(X^n) = \dfrac{1}{B(\alpha, \beta)} \int_0^1 x^n x^{\alpha - 1} (1-x)^{\beta - 1}dx \\ = \dfrac{1}{B(\alpha, \beta)} \int_0^1 x^{(\alpha+n) - 1} (1-x)^{\beta - 1}dx\\ = \dfrac{B(\alpha + n, \beta)}{B(\alpha, \beta)}. \] Concluimos utilizando la relación entre la funcion beta y la funcion gamma, \(B(x, y) = \Gamma(x)\Gamma(y)/\Gamma(x+y)\). Los casos particulares de valor esperado y varianza se obtienen evaluando la fórmula general en \(n=1\) y \(n=2\), utilizando \(Var(X) = E(X^2) - (E(X))^2\). \(\square\)
Sean \(X_1, \ldots, X_n\) v.a. iiid con distribución \(Bernoulli(p)\). Sabemos que la v.a. \(Y = \sum_i X_i\) tiene distribución \(Binomial(n, p)\).
A continuación para la estimación Bayesiana suponemos (se debe aclarar en la letra) que la ditribucion a priori de \(p\) es la distribución \(Beta(\alpha, \beta)\). Haremos uso del repaso de las propiedades destacadas de la distribución beta hecho anteriormente.
La probabilidad conjunta de \(Y\) y \(p\) es igual a la probabilidad condicional por la probabilidad marginal, \(f(y\vert p) \times \pi(p)\),
\[ f(y, p) = \left[\binom{n}{y} p^y (1-p)^{n-y} \right]\left[ \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1} \right] \\ = \binom{n}{y} \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{y+\alpha-1}(1-p)^{n-y+\beta-1}. \]
Realicemos el cálculo de la distribución marginal de \(Y\)
\[ f(y) = \int_0^1 f(y, p) dp = \binom{n}{y} \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \int_0^1 p^{y+\alpha-1}(1-p)^{n-y+\beta-1} dp \\ = \binom{n}{y} \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}B(y+\alpha, n-y+\beta) \\ = \binom{n}{y} \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\dfrac{\Gamma(y+\alpha)\Gamma(n-y+\beta)}{\Gamma(n+\alpha+\beta)}. \\ \]
La distribución a posteriori (la distribución de \(p\) dado \(y\)) es
\[ f(p\vert y) = \dfrac{f(y, p)}{f(y)} = \dfrac{\Gamma(n+\alpha+\beta)}{\Gamma(y+\alpha)\Gamma(n-y+\beta)}p^{y+\alpha-1}(1-p)^{n-y+\beta-1}\\ = \dfrac{1}{B(y+\alpha, n-y+\beta)}p^{y+\alpha-1}(1-p)^{n-y+\beta-1}.\\ \] Identificamos a esta distribución como la distribución \(Beta(y+\alpha, n-y+\beta)\). Recuerde que \(p\) es la variable e \(y\) se trata como fijo.
Utilizando el estimador para \(p\) como el valor medio de la distribución a posteriori, y recordando la fórmula para el valor medio de una distribución beta, tenemos que:
\[ \hat{p}_B = \dfrac{y+α}{α+β+n}. \]
Sea \(Y = \sum_i X_i\).
El MSE del estimador Bayesiano, \(\hat{p}_B\), de \(p\), es por definición
\[ E_p(\hat{p}_B - p)^2 = Var_p \hat{p}_B + (Bias_p \hat{p}_B)^2 \\ = Var_p \left( \dfrac{Y+α}{α+β+n} \right) + \left( E_p\left( \dfrac{Y+α}{α+β+n} \right) - p \right)^2. \]
Recordemos que la varianza de una v.a. constante es cero, y que \(Var(aX) = a^2 Var(x)\). Recordemos también que la varianza de la suma de v.a. no correlacionadas es la suma de las varianzas, y que si \(X\) tiene distribución de Bernoulli de parámetro \(p\), entonces \(Var(X) = p(1-p)\). Deducimos que el primer término de la derecha es
\[ Var_p \left( \dfrac{Y+α}{α+β+n} \right) = \dfrac{1}{(α+β+n)^2} Var_p Y \\ \dfrac{1}{(α+β+n)^2} np(1-p). \]
El segundo término de la derecha lo trabajamos de manera análoga, dado que \[ E_p \left( \dfrac{Y+α}{α+β+n} \right) = \dfrac{np + α}{α+β+n}. \]
Obtenemos que el MSE para este estimador Bayesiano es
\[ E_p(\hat{p}_B - p)^2 = \dfrac{np(1-p)}{(α+β+n)^2} + \left( \dfrac{np + α}{α+β+n} - p\right)^2. \]
Tomamos \(\alpha = \beta = \sqrt{n/4}\). Debemos sustituir estos valores en la fórmula de \(E_p(\hat{p}_B - p)^2\) hallada en la parte anterior.
Realicemos el algebra con la ayuda de SageMath. Se puede evaluar este código en una celda de Sage en el programa online SageCell.
sage: var('n, p, alpha, beta')
sage: expr = n*p*(1-p)/(alpha + beta + n)^2 + ((n*p + alpha)/(alpha + beta + n) - p)^2
sage: expr(alpha=sqrt(n/4), beta=sqrt(n/4)).simplify_full()
1/4*(n + 2*sqrt(n) + 1)/(n^2 + 4*(n + 1)*sqrt(n) + 6*n + 1)Nótese esta cantidad es independiente del parámetro \(p\), como queriamos probar.
De hecho podemos simplificar aún más esta expresión con la ayuda del método canonicalize_radical:
sage: expr.canonicalize_radical()
1/4/(n + 2*sqrt(n) + 1)que es \[ \dfrac{1}{4(1+\sqrt{n})^2}. \]
Utilizando estos valores de \(\alpha\) y de \(\beta\), el estimador Bayesiano del parámetro \(p\) es
\[ \hat{p}_B = \dfrac{Y + \sqrt{n/4}}{n + \sqrt{n}}. \]
Observación. Cabe preguntarse cómo conocer averiguar desde un principio los valores de \(\alpha\) y \(\beta\) necesarios para que el MSE sea constante respcto a \(p\). Con Sage podemos hacer el cálculo siguiente:
sage: solve(expr.derivative(p).simplify_full()==0, p)
[p == 1/2*(2*alpha^2 + 2*alpha*beta - n)/(alpha^2 + 2*alpha*beta + beta^2 - n)]Este cálculo equivale a hacer \(\dfrac{\partial MSE(\hat{p}_B)}{\partial p} = 0\).
Aquó solve me dice que para que sea cero dicha derivada parcial, preciso que la
cantidad \(2α^2 + 2αβ - n\) sea cero. Es fácil
ver que esto se cumple eligiendo \(\alpha = \beta = \sqrt{n/4}\). Hay otras elecciones posibles,
pero la particularidad del caso \(\alpha = \beta\) es que la pdf es simétrica respecto a \(1/2\).
En este ejercicio calculamos la distribución a priori Beta de parámetros \(\alpha = \beta = \sqrt{n/4}\). Sea \(\hat{p} = \bar{X}\) el MLE asociado a la Bernoulli (este cálculo se realizó en el teórico). El MSE asociado a \(\hat{p}\) es
\[ E_p(\hat{p}-p)^2 = Var_p \bar{X} = \dfrac{p(1-p)}{n}. \]
¿Qué estimador conviene mas? Consideremos esta pregunta realizando el gráfico de cada MSE para dos tamaños muestrales distintos.
Primero definimos las funciones en R:
MSE_Bayes <- function(n){n / (4*(n+sqrt(n))^2)}
MSE_MLE <- function(n, p){p*(1-p)/n}Para el caso de muestra chica n=4:
# caso muestra chica
n = 4
plot(function(p){MSE_MLE(n, p)}, 0, 1, ylab="", xlab="p")
abline(h = MSE_Bayes(n))
mtext(paste("n =", n))
Para valores de \(n\) chicos, \(\hat{p}_B\) es más conveniente, a menos que tengamos una fuerte sospecha de que el valor de \(p\) se encuentra cerca de \(0\) o de \(1\).
Para el caso de muestra grande n=400:
# caso muestra grande
n = 400
plot(function(p){MSE_MLE(n, p)}, 0, 1, ylab="", xlab="p")
abline(h = MSE_Bayes(n))
mtext(paste("n =", n))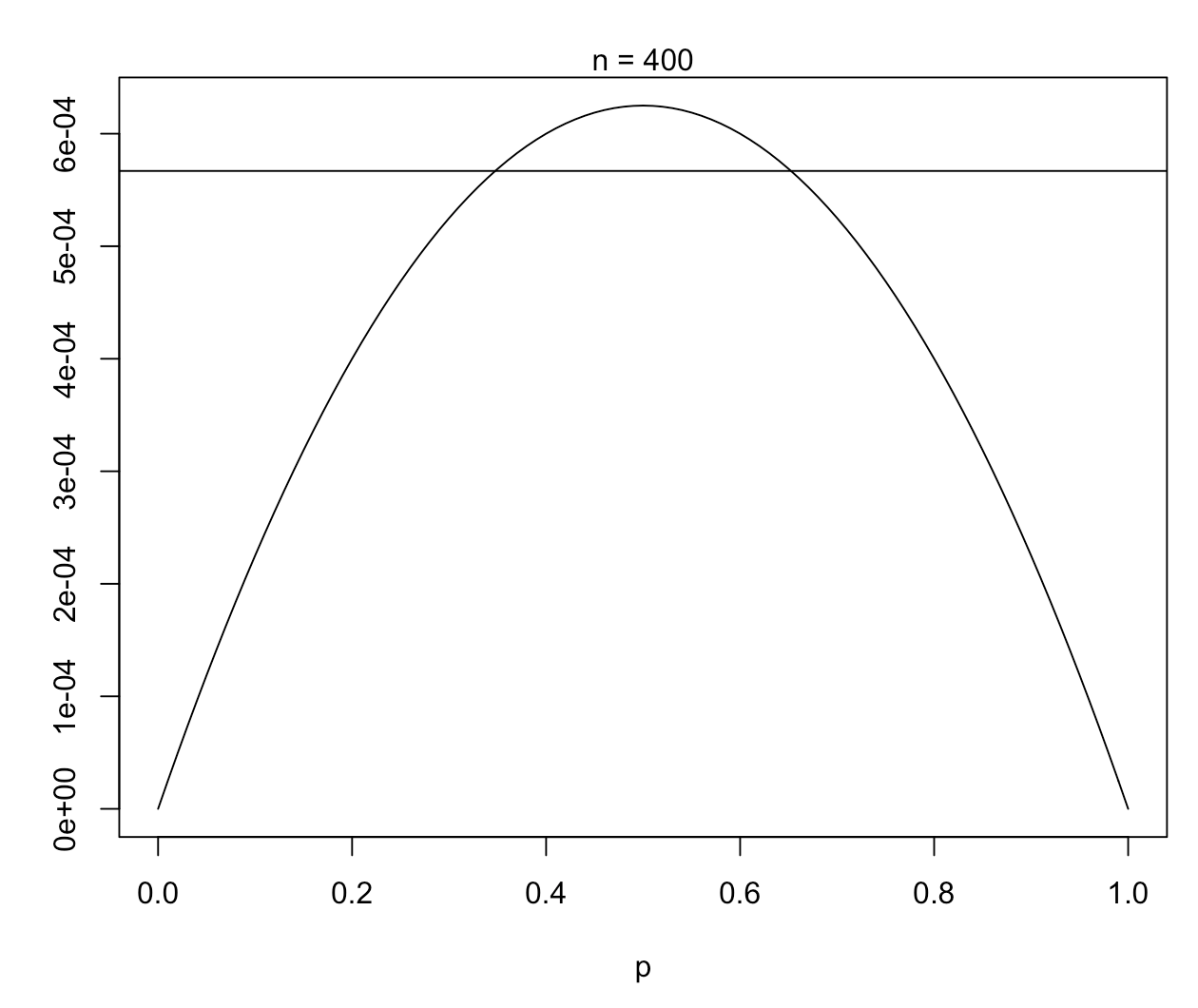
Para valores de muestra grandes, \(\hat{p}\) es en general mejor estimador.
La información que nos da el MSE junto con la información que tengamos del problema nos puede ayudar a decidir cuál estimador tomar para un problema dado.